复兴高级中学2020-2021学年度第一学期高中三年级数学周测卷二
1、填空题
1.已知
,则
________.
2.函数
的单调递增区间是________.
3.函数
的图象的对称中心是P
13.若
则
的元素个数为
A.0 B.1 C.2 D.3
14.设
为常数,若函数
存在反函数,则方程
A.有且仅有一个实根 B.至少一个实根
C.至多一个实根 D.没实数根
15.关于函数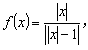
给出以下四个命题:
①当
时,单调递减目没最值；
②方程
肯定有解；
③假如方程
有解,则解的个数肯定是偶数；
④是偶函数且有最小值。
其中的真命题是
A.②④ B.④ C.②③ D.③④
16.已知
是概念域为R的三个函数,对于下列命题:
①
均为增函数,则中至少有一个增函数；
②若均是以T为周期的函数,则均是以T为周期的函数.
下列判断正确的是
A.①和②均为假命题 B.①和②均为真命题
C.①为假命题,②为真命题 D.①为真命题,②为假命题
3、解答卷
17.
已知函数
判断函数的奇偶性,并说明理由；
证明:函数在R上不是增函数。
18.
已知函数
的图像经过点A,B.
试确定
；
若不等式
在
时恒成立,求实数
的取值范围。
19.已知
和
，若他们的概念域均为
.
求函数的最小值
；
若对于任意的
,不等式
恒成立,求实数
的取值范围。
20.
已知函数是单调递增函数,其反函数是
.
若
求并写出概念域M；
对于的和M,设任意
,求证:
；
求证:若和有交点,那样交点肯定在
上。
21.
已知函数
在区间
上的最大值为4,最小值为1,记：
求实数
的值；
若不等式
对任意
恒成立,求实数
的取值范围；
对于概念在上的函数
,设用任意
的将划分成
个小区间,其中
若存在一个常数M＞0,使得
恒成立,则称函数为在上的有界变差函数。试证明函数是在
上的有界变差函数,并求出M的最小值。
